STRONGLY CORRELATED QUANTUM MATERIALS

• In materials science, strongly correlated materials are materials in which electron–electron interactions (correlations) play a dominant role in determining the material’s physical and chemical properties. These interactions are so strong that they cannot be accurately described by conventional theories like standard density functional theory (DFT) or the nearly-free-electron model.
• In strongly correlated materials, the motion of one electron is highly dependent on the positions and states of other electrons, often leading to: Mott insulating behavior, Unconventional superconductivity, Heavy fermion behavior. Magnetic frustration, Orbital ordering, and Ferromagnetism

Strongly correlated materials

The full many-body Hamiltonian, which includes all electronic and nuclear degrees of freedom, is nearly impossible to solve exactly due to its complexity. To make the problem tractable, various approximations are introduced—such as the Born-Oppenheimer approximation (freezing nuclear motion), model Hamiltonians like the Hubbard model, or mean-field approaches like Density Functional Theory (DFT). In the DMFT framework, we do not solve the original Hamiltonian directly but instead solve the simplified Hubbard model in a self-consistent manner.

To incorporate strong on-site Coulomb interactions more effectively, the DFT+U method is often employed as an extension of standard DFT, typically on top of LDA or GGA.

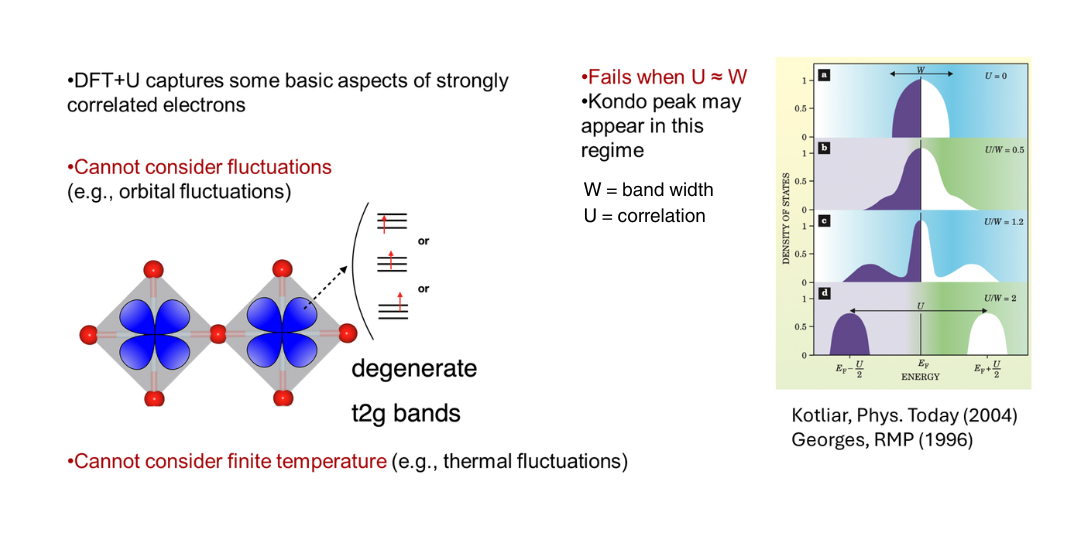
To address the dynamic correlation effects beyond the static treatment of DFT+U, advanced methods like Dynamical Mean Field Theory (DMFT) or Density Matrix Renormalization Group (DMRG) are required.

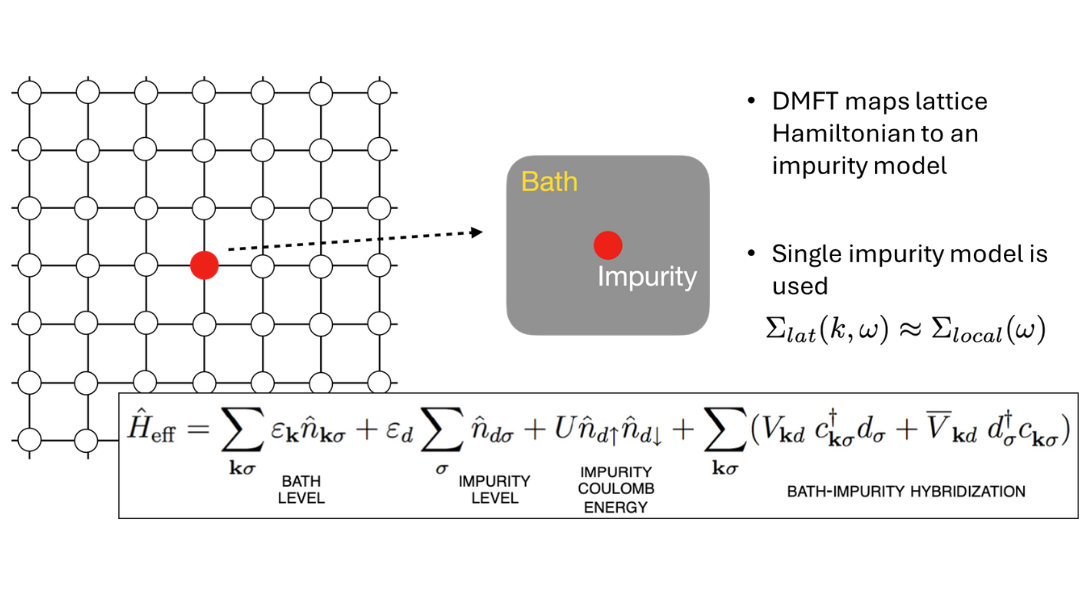
DMFT maps lattice Hamiltonian to an impurity model

• Wannier Hamiltonian is obtained from DFT, and it is used as initial lattice Hamiltonian
• Continuous Quantum Monte Carlo (CTQMC) is used for self-consistent calculation for self energy

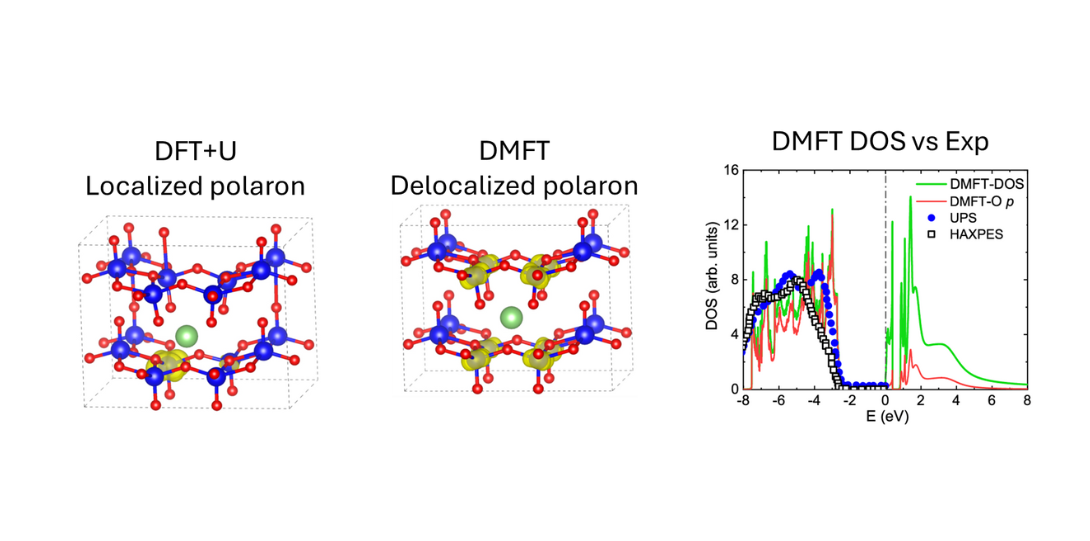
We use DFT+DMFT to uncover the dual nature of polarons in Li-doped α-V₂O₅—free and bound—and their impact on conduction. Unlike DFT+U, our method captures the delocalized bound polaron as the ground state and reveals a Burstein-Moss shift driven by Li doping. This work demonstrates the power of many-body theory in describing strongly correlated cathode materials.

• Nam Nguyen, Alex Taekyung Lee, Anh T. Ngo and Hyowon Park. Impact of structural distortions on the correlated electronic structure of orbital-selective Mott insulating Na₃⁢Co_2⁢SbO₆ under strain. Phys. Rev. B 112, 085157 (2025)
• Stability and diffusion of oxygen vacancies in LaNiO3: a DMFT study, submitted
• Delocalized polaron and Burstein-Moss shift induced by Li in α-V2O5, A DFT + DMFT study: Physical Review B, 108, 205122 (2023)
• Effect of off-diagonal elements in the Wannier Hamiltonian on DFT + DMFT for low-symmetry materials: Physical Review B 108, 205146 (2023)
• Study of spin-charge-lattice coupling in covalent: Phys. Rev. B, 101, 195125 (2020)

• Ab initio Density Matrix Renormalization Group (DMRG) is a powerful numerical method for studying quantum many-body systems, particularly in one-dimensional (1D) or quasi-1D geometries. It provides highly accurate solutions by variationally optimizing a matrix product state (MPS) representation of the wavefunction.
• DMRG is especially effective at capturing strong correlations and entanglement in low-dimensional systems, making it a leading tool for investigating spin chains, 1D Hubbard models, and molecular systems in quantum chemistry. While its computational efficiency declines in higher dimensions, DMRG remains a gold standard for 1D systems due to its ability to handle large Hilbert spaces with controlled accuracy.

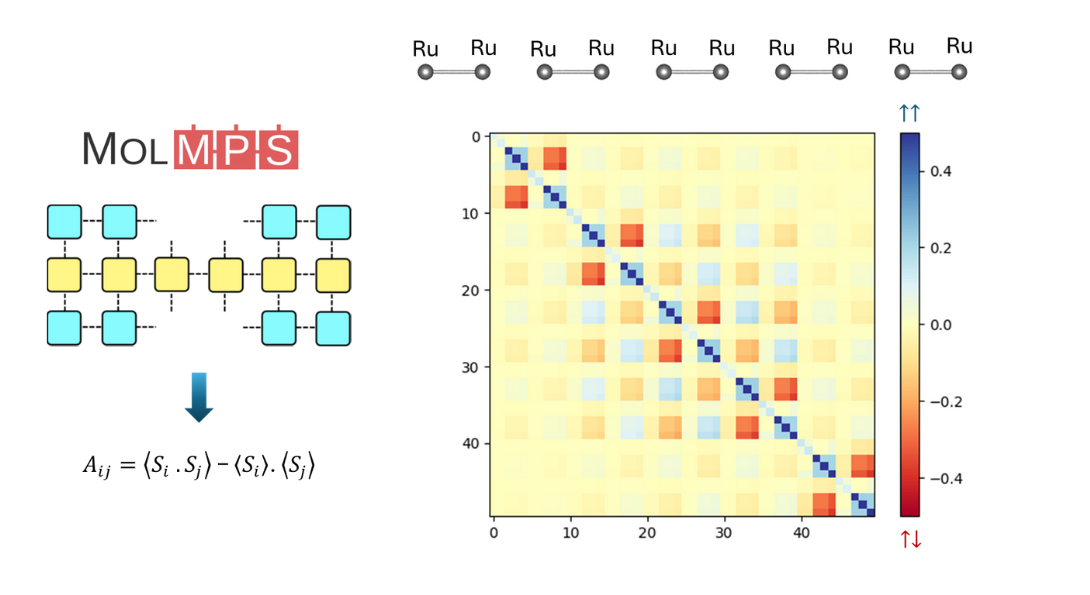
• We study the transition metal (TM) atom chains within DFT+U and DFT+DMRG
• We consider 3d and 4d transition metals, such as Fe, Co, Ni, Ru, etc
• We focus on the dimerization of TM ions, magnetic order and frustration, quantum entanglement, etc

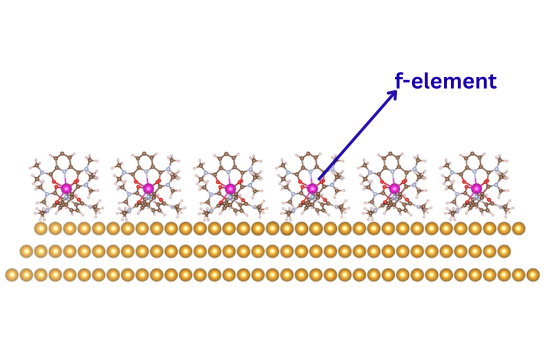
• Molecules containing f-elements, such as lanthanides or actinides, exhibit rich quantum behavior due to the presence of highly localized f-electrons. These electrons give rise to strong spin–orbit coupling, large magnetic moments, and complex multiconfigurational electronic structures that challenge conventional computational methods.
• Because of their unique properties, f-orbital molecules are of great interest for applications in single-molecule magnets, molecular spintronics, and quantum information science. In particular, their long spin coherence times and strong magnetic anisotropy make them promising candidates for molecular qubits and high-density magnetic storage.
• Our research focuses on understanding the electronic structure, magnetic behavior, and spin-state transitions of these systems on the Gold surface using advanced methods such as DFT+U. We also simulate X-ray absorption spectra (XAS) using both atomic multiplet theory and time-dependent DFT (TDDFT), enabling direct interpretation and explanation of experimental XAS results.